Урок 12. Непериодические бесконечные десятичные дроби

https://resh.edu.ru/subject/lesson/6916/main/ 

Рациональное число (лат. ratio «отношение, деление, дробь») — число, которое можно представить обыкновенной дробью. , числитель. — целое число, а знаменатель. — натуральное число. 

Рассмотрим положительную бесконечную десятичную дробь 0,1011011101111…

У этой дроби нет группы цифр, являющейся периодом. Эта дробь непериодическая.

Примеры бесконечных непериодических дробей

0,010010001…

17,1234567891011…

Поставив перед положительной дробью знак «–», получим отрицательную дробь.

Например, дробь

– 0,1001000100001…

является отрицательной бесконечной непериодической дробью.

Обнаружены новые числа, которые раньше не встречались. Эти новые для вас числа называют иррациональными. 

Число, которое можно записать в виде бесконечной непериодической десятичной дроби, называют иррациональным числом.

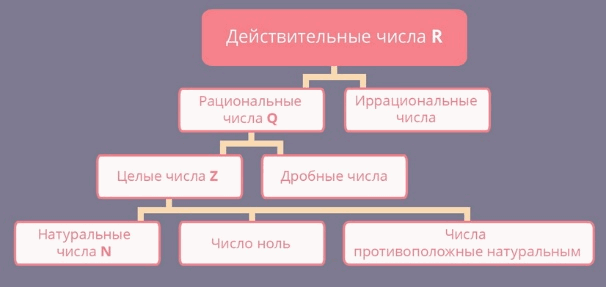
Рациональные и иррациональные числа называются действительными числами.

Любое действительное число представляется в виде бесконечной десятичной дроби.

Если число – рациональное, то дробь – периодическая, а если иррациональное, то дробь – непериодическая.

Рассмотрим на примере

Рассмотрим №991. Записать четыре числа

а) натуральных (те, которые используются при счете): 1,2,3,4

б) положительных (больше 0): 2; 2,5; 10; 250

в) отрицательных (меньше 0): -1; -3,6; -15; -100

г) целых: -2, 0, 3, 14

д) рациональных (которые можно представить в виде обыкновенной дроби): -10/1; -2,5; 6; 47,2

е) иррациональных (которые нельзя представить в виде обыкновенной дроби): -0,142864621; 2,3589765; 15,34687169; 1,3211236

ж) четных (которые делятся на 2): 4,6,8,10

з) нечетных (которые не делятся на 2): 5,7,9,11

и) простых (которое делится на 1 и само на себя): 2,3,5,7

к) составных (которое содержит в себе больше, чем 2 множителя): 4, 16, 27, 28

л) кратных 3: 6,9,12,15

м) кратных 2 и 5: 10, 20, 30, 50

Домашнее задание: Записать свои примеры №991(и,к,л,м), 992 (г,д,е)