Урок 14. Действительные числа
Мы с вами уже знаем из курса математики, что при объединении положительных, отрицательных чисел и 0 получается множество целых чисел. По аналогии мы можем объединить рациональные числа и иррациональные – получаем множество действительных чисел. А, значит, любое действительное число можно представить в виде бесконечной десятичной дроби: если число рациональное, то дробь периодическая, если иррациональное, то непериодическая.
Как нам уже известно в записи десятичной дроби слева от запятой расположена целая часть, справа числа по разрядам, начиная с десятых.
Для записи десятичных дробей в общем виде используются буквы. Например: пусть дана положительная бесконечная десятичная дробь. α0 – целая часть, равная 0 или целому числу, α1 α2 α3… αn…- цифры по разрядам после запятой.
Действительные числа называют противоположными, если они отличаются только знаком.
Абсолютной величиной (модулем) называют
Рассмотрим №1004
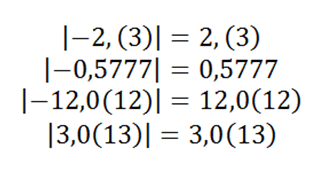Рассмотрим №1005
а) противоположное число 2,5(3) = -2,5(3)
б) противоположное число -1,(72) = 1,(72)
Рассмотрим №1007
а) округлим числа до 0,1, тогда получится
12,3-0,1 = 12,2
в) 4,2-1,1 = 3,1
Рассмотрим №1009
а) 11,(4)-7,3
Округлим до 0,001 и найдем разность
11,444-7,300 = 4,144
в) 7,(93)-2,(39)
7,(93) ≈ 7,939393 ≈ 7,9393 (так как 4 цифра после запятой меньше чем 5, то 3я цифра после запятой не изменяется)≈ 7,939
2,(39) ≈ 2,3939 (так как 4я цифра больше, чем 5, то 3я цифра увеличивается на 1) ≈2,394
Тогда:
7,939-2,394 = 5,545
Домашнее задание: Прочитать стр 200-202, письменно №1005(в,г), 1007(б), 1009(б)
